

Recall, a linear function is a polynomial of degree one or zero. Furthermore, a linear function is a function where there is a constant rate of change or there is a constant ratio between the change in the inputs to the change in the corresponding outputs. For the sake of this exploration, the input and output values will ve donted by the variables x and y respectively.
For example: f(x) = 6x+5
Now, let's think about the following linear functions:
f(x) = x+2
g(x) = x-6
Because these functions are both linear, it makes sense that when graphed individually each fucntion will produce a straight line. The question now is what happens when these functions are added together? What will their graph look like?
Let's call the sum of f(x) and g(x), h(x):
Now,
h(x) = f(x) + g(x)
h(x) = (x+2) + (x-6)
h(x) = 2x-4
Thus, h(x) is a linear function because h(x) is a degree 1 polynomial and has a constant rate of change of 2. Below is a graph of f(x), g(x), and h(x).
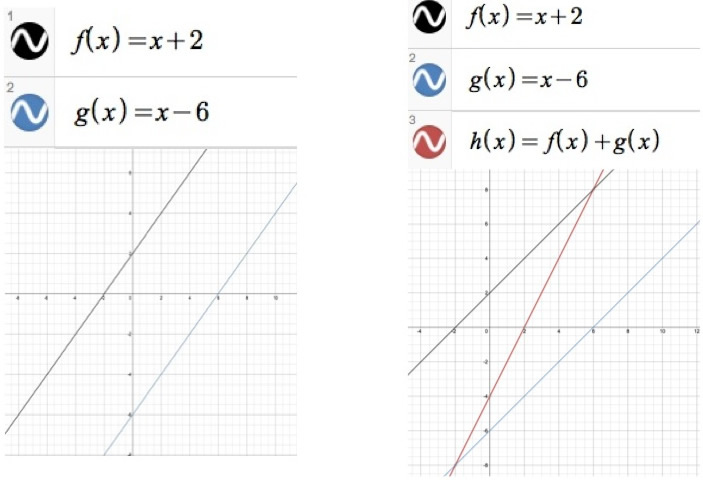
In the case presented, both f(x) and g(x) produced graphs whose lines were parallel. This is because the slope of these lines were the same. However, for any two linear functions, their sum will produce another linear function. This can be explored more by clicking the link below which will provide two functions with varying coefficents. This can also be explained by algebra. For any linear functions f(x) and g(x), the only possible results are a function with degree 1 and a function with degree 0.
Multiplication:
Now consider the following functions:
f(x)= x+2
g(x)= x+5
Individually, these graph of these functions will be represented by a straigh line. However, what happens when the two linear functions are multiplied?
h(x) = f(x) g(x)
h(x) = (x+2)(x+5)
h(x) = x^2 + 5x + 2x+ 10
h(x) = x^2 + 7x +10
By multiplying f(x) and g(x), it follows that h(x) is not a linear function. As a matter of fact, h(x) is a quadratic function, meaning the degree of h(x) is 2.
Below is a graph that illustrates f(x), h(x), and g(x).
You can manipulate the graph here to see that the same results will occur.
Division:
Consider the following functions:
f(x) = x+6
g(x)= x+3
Both functions, f(x) and g(x) are linear; however, let’s what happens when these functions are divided.
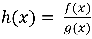
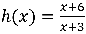
Below is the graph of f(x), g(x), and h(x).
This graph is obviously not linear; thus, h(x) is not linear. The graph of this function is actually hyperbolic. Taking a closer look at h(x) and its graph will explain why it behaves as it does.
First, we can look at the domain of this function. The domain of a function is simply the set of all input values which produce an output value. For this particular function, the domain consists of all real numbers except -3. This is because when x=-3, the denominator of the function is 0 which yields an undefined output. This gives a vertical asymptote at x=-3.
Now, we can look at the range of h(x). From the graph, it is obvious that as the function approaches 0 from the left, the y-values approach 1. The same can be said as the function approaches 0 from the right, the y-values approach 1. Thus, it seems like there is a horizontal asymptote at y=1.
The degrees of both f(x) and g(x) are the same; thus, the horizontal asymptote is 1, y=1.
The values within these asymptotes can be found by plugging in values for h(x).
Thus, the division of linear functions will lead to a hyperbolic function except when f(x) is a multiple of g(x) or if f(x) or g(x) is a constant function.
Click Here to try different functions to see that the exceptions just stated are linear.
Composition:
Let’s try a different set of functions.
Suppose
f(x)= x+9 and g(x)= x-1.
Now we will compose these functions. h(x)=f(g(x))
h(x)=(x-1)+9
h(x)= x+8.
h(x) is a linear function. The graph of f(x), g(x), and h(x).
Explore the graph with Desmos.
In all cases, the composition of two linear functions will result in a linear function. We can prove this by looking at two linear functions with arbitrary coefficients and constants.
Let f(x)=ax+b and g(x)=cx+d where a, b, c, and d are real numbers
Now when h(x)= f(g(x))
h(x)= a(cx+d)+b
h(x)= acx+ad +b
h(x)=(ac)x+(ad+b)
Hence h(x) is a linear function.